Learning image
segmentation and recognition
Abstract
Image
segmentation is often
treated as an unsupervised task.
Segmentation by human, in contrast, relies heavily on memory to produce
an object-like clustering, through a mechanism of controlled
hallucination. This paper presents a learning algorithm for
memory-driven
object
segmentation and recognition. We propose a general spectral graph
learning algorithm based on gradient descent in the space of graph
weight matrix using derivatives of eigenvectors. The gradients are
efficiently
computed using the theory of implicit functions. This algorithm
effectively
learns a graph network capable of memorizing and retrieving
multiple patterns given noisy inputs. We demonstrate the validity of
this approach on
segmentation and recognition tasks, including geometric shape
extraction, and hand-written digit recognition.
Encoding
Recognition and
Segmentation with Spectral Graph Cuts
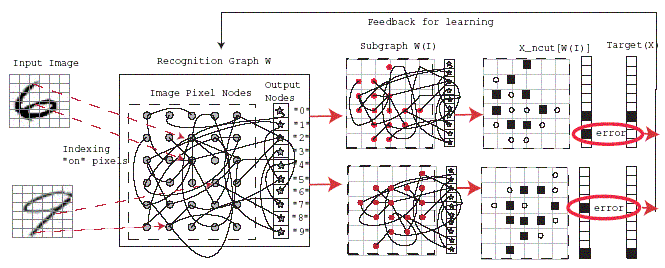
A Spectral Memory Graph consists of a set nodes (pixels, features,
class labels), a set of edges indicating which nodes are connected, and
a weight function W specifying their pair-wise similarity. Given an
input image I, we detect a subset of “on” features, inducing the weight
submatrix W(I). The output for both segmentation and recognition in
image I is encoded with Ncut eigenvector Xncut, defined
as the second eigenvector of the system W(I)X = µ DW(I)X,
where DW = diag(W1). The aim is to learn W either
directly in the coefficient space (Wij) or
through a parameterization. Three
applications are detailed below to illustrate the concept.
Learning
algorithm
We use the following error
functions for learning images {I}:
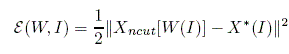
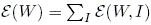
where X*(I) is the target and Xncut[W(I)]
is the output (Ncut eigenvector of W(I)). Our goal is to minimize the
error function by gradient descent :
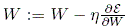
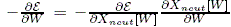
The main difficulty is to compute this gradient term, which involves
the partial derivatives of eigenvectors w.r.t. all the coefficients Wij.
We show in
the paper how to do this efficiently in exact analytical form.
Applications
1.
Segmentation and Recognition of noisy digits
We show how to apply the algorithm to segmentation and
recognition of noisy digits (taken from MNIST database).
Spectral
memory Graph for digit segmentation and recognition



Results: Top row = Input images ; middle
row = target images ; bottom row =
learned segmentation
2.
Learning boolean functions
We demonstrate that we can learn non-linearly separable functions such
as XOR. Here a network is trained to learn simultaneously AND, OR, XOR.
The graph nodes are {x, ¬x, y, ¬y, zAND, zOR, zXOR}, and the
weight matrix W is of size 7x7 (49 parameters to learn). Note that a
seperate network was also trained with just {x,
¬x, y, ¬y, zXOR}.
Learning functions AND, OR, XOR. Graph
nodes:
{x, ¬x, y, ¬y, zAND, zOR, zXOR}. Ncut on a subgraph extracted
from the learned graph W encodes the desired logical operations.
3.
Learning geometrical shapes
We learned a parameterization of the weights that is
invariant by translation, allowing us to learn square shapes with a
very limited training set. The graph nodes are pairs of edgelet
position xi and edglet angle µj. The
graph weights W(xi,µj ; xi′ ,µj′ ) = f(xi′ −xi,
µj′ −µj) are learned with 50 training examples on image
size 100 × 100. f has a total of 4096 free parameters to be
learned (edgelet position displacements ±dx=±dy =16,
edgelet orientation displacements ±dµ = 4).
|
|
 |
 |
 |
| |
training set |
testing set |
testing on real images |
 Back to my
home page
Back to my
home page





